Bubble Sort

The Sorting Algorithm That Sorts... Eventually!

Problem Definition

Given an array of unsorted values, how can we sort them so that they end up in ascending order?

Theory

The bubble sort makes multiple passes through a list. It compares adjacent items and exchanges those that are out of order. Each pass through the list places the next largest value in its proper place. In essence, each item “bubbles” up to the location where it belongs.

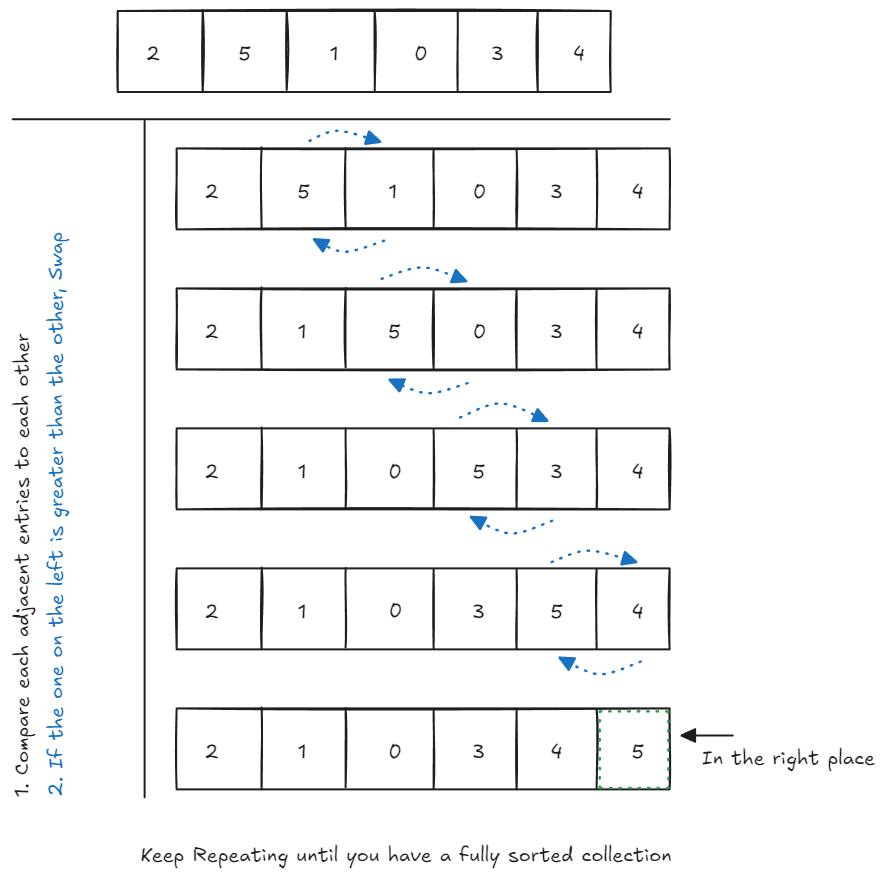
1. Point to two consecutive values in the array. (Initially, start by pointing to the array’s first two values)
2. Compare the first value to the second one.
3. If the two items are out of order i.e. the first item is larger than the second item, swap them.
4. Move the pointer one cell to the right.
5. Repeat the previous steps until you reach the end of the array.

Typically you’ll need an  $n-1$ of pass-through to ensure that the collection is sorted. because the last path-though will ensure placing two items in their right place. which is the first and the second item.

Sorting in Ascending vs Descending order

You can easily control how the collection is sorted by controlling the swap condition.

Implementation

There are several ways to implement this simple algorithm, all with the same time and space complexity in the worst case scenario. The variations exist to highlight that the underlying algorithm —not its specific implementation— is what truly matters. However, some implementation are more optimized for specific scenarios than the others.

1. Using Nested Loops

This is the most straightforward way to implement Bubble Sort: two nested loops that repeatedly compare and swap adjacent elements. It runs through the entire array on every pass, even if it’s already sorted.

public int[] Sort(int[] collection)
{
 for (int i = 0; i < array.Length; i++)
 {
  for (int j = 0; j < array.Length - i - 1; j++)
  {
   if (array[j] < array[j + 1]) continue;
   (array[j], array[j + 1]) = (array[j + 1], array[j]);
  }
 }
 return array;
}

• Best case: $O(N^2)$
• Average case: $O(N^2)$
• Worst case: $O(N^2)$

2. Optimized for early exists

This version adds a small improvement: a swapped flag that breaks the loop early if no swaps were made during a pass. This makes it much faster when the array is already (or almost) sorted.

public int[] Sort(int[] collection)
{
 bool swapped = false;
 var n = array.Length - 1;
 for (int i = 0; i < n; i++)
 {
  for (int j = 0; j < n - i; j++)
  {
   if (array[j] > array[j + 1])
   {
    (array[j], array[j + 1]) = (array[j + 1], array[j]);
    swapped = true;
   }
  }
  if (!swapped) break;
 }
 return array;
}

• Best case: $O(N)$
• Average case: $O(N^2)$
• Worst case: $O(N^2)$

More efficient — ideal for nearly sorted data.

Analysis

Space Complexity

It’s always $O(1)$ since the auxiliary space the extra space or the temporary space that an algorithm uses. doesn’t increment in relation to the input size. note that int[] array = collection doesn’t actually consume extra space, because it’s more or less creating a reference to an existing array (in c# of course).

Time Complexity

In the worst case, Bubble Sort is given a completely reversed array — the exact opposite of sorted. Every element needs to “bubble” all the way to its correct position, one swap at a time.

The outer loop runs $N - 1$ times. On each pass, the inner loop compares fewer elements: starting with $N - 1$, then $N - 2$, and so on, down to $1$.

This forms a summation:

\[(N - 1) + (N - 2) + ... + 1 = N(N - 1)/2\]

Which gives a worst-case time complexity of $O(N^2)$.